In 1998 Vorobyev & Osorio published the influential paper on ‘Receptor noise as a determinant of colour thresholds’. In that paper the authors formally introduce the Receptor Noise Limited (RNL) model. The model states that, given a range of assumptions (see below), colour discrimination is determined by the noise inside the photoreceptors of a visual system, the relative abundance of these photoreceptors and the opponent mechanisms by which these photoreceptor signals are processed.
Assumptions of the RNL model (Vorobyev & Osorio 1998):
- For a visual system with n receptor channels, colour is coded by n-1 unspecified colour opponent mechanisms; the achromatic signal is disregarded.
- Colour opponent mechanisms give zero signal for stimuli that differ from the background in intensity only.
- Thresholds are set by receptor noise, and not by opponent mechanisms.
The authors provide a list of constraints on the conditions where the model may be used (Vorobyev & Osorio 1998):
- Large static stimuli must be presented under bright illumination (to suppress the contribution of an achromatic channel)
- The background must be achromatic (colour opponent mechanisms give zero signal)
These assumptions and constraints are important to keep in mind when choosing discrimination thresholds or interpreting numerical output of the QCPA.
Equations for a dichromat:
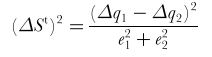
Equations for a trichromat:
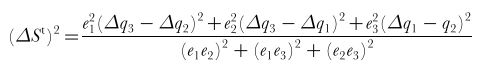
ΔSt is the discrimination threshold defined by the quantum catch of the first receptor channel (Δq1), the second one (Δq2)and the third one (Δq3) and the respective noise level of these channels (e1, e2 & e3). From Vorobyev & Osorio 1998
Equations for a tetrachromat:
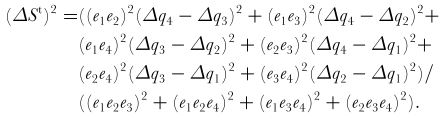
ΔSt is the discrimination threshold defined by the quantum catch of the first receptor channel (Δq1), the second one (Δq2), the third one (Δq3) and the fourth one (Δq3) and the respective noise level of these channels (e1, e2, e3 & e4). From Vorobyev & Osorio 1998
ΔSt is often referred to as a ‘Just noticable difference’ (JND). It depends on the threshold criterion and is simply the euclidian distance of a chromatic stimulus to the achromatic point in colour space. Vorobyev & Osorio 1998 state that usually ΔSt = 1 at 75% correct choice (In a pairwise choice paradigm, under the listed assumptions and conditions). While this 75% threshold criterion indeed has been shown to correlate with a ΔSt ≈ 1 in a number of species such as bees, humans and a number of birds (Kelber et al. 2003) it remains untested in most other animals. This is very often not the case, given that receptor noise and opponent channels remain unknown for most animal species and many colour discrimination tasks (Such as the ones performed by QCPA and many studies) do not comply with the assumptions and constrains posed by the RNL model. i.e. most people use the RNL to compare colours with colours concerning small intricate colour patches using visual systems for which both receptor noise levels and opponent processes are conservative guesswork and, to make it even worse, using spectral sensitivities borrowed from another species. A fairly large deviation from the assumptions and conditions, one could say.
As a result, many studies use conservative discrimination thresholds of ΔSt = 3. Which, until behaviourally tested, remain conservative guesstimates.
The linear and the log-transformed RNL model:
The Euclidian distance of a colour stimulus to an achromatic background can be calculated using both actual cone catch quanta or their log-transformed values (Vorobyev et al. 1998, 2001). The later bears the advantage of turning the channel-specific noise into a Weber fraction. Meaning, it includes the assumption that receptor noise in a photoreceptor is independent of the stimulus intensity which makes the ΔS values more uniform across colour space. As a result, it is only advised to use the linear RNL model in very close proximity to the achromatic point (i.e. comparing a weakly chromatic colour to an achromatic background).
Using the RNL model for achromatic (luminance) discrimination:
Siddiqi et al. (2004) have introduced the idea that the concept of the RNL model could also be applied to describe psychophysical discrimination thresholds for luminance contrast as the receptor noise and their abundance likely also determine an animal’s ability to discriminate between luminance intensities.
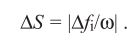
However, we like to point out that achromatic and chromatic vision differ substantially from each other and drawing paralleles between them (e.g. guessing luminance discrimination thresholds based on colour discrimination) should only be done with caution and preferably using extensive ω validation (van den Berg et al. in prep). Despite increasing popularity the application of the RNL model for luminance discrimiantion, behavioural validation remains largely inexistent.
ΔS vs. JND what’s the difference?
The term JND (‘Just noticable difference’) means a contrast threshold that correlates with a discrimination threshold criteria. E.g. the contrast at which an animal is able to make the correct choice in a pairwise paradigm 75% of the time (Vorobyev & Osorio 1998). However, while in theory this threshold is located at ΔS≈1, this involves a whole range of rarely met assumptions and conditions outlined above. Therefore, the point at which an animal is able to meet the threshold criteria is often above ΔS≈1 (but it can also be below 1). Furthermore, chromatic (and achromatic) discrimination is known to be non-linear in relation to stimulus intensity. i.e. while an animal can discriminate a weakly chromatic stimulus from an achromatic background at ΔS≈1 it may struggle to find the difference between two extremely chromatic stimuli with a contrast of ΔS≈4.
In summary: While a JND can correspond to a fraction or multiples of 1 ΔS (depending on where you are in colour space) it is incorrect to equate any distance in colour space to a JND without behaviourally testing how many ΔS correspond to a JND. It is also not advised to use multiple JNDs e.g. if a JND = 1.2 ΔS near the achromatic point, it doesn’t mean that a distance of 3.6 ΔS = 3 JNDs anywhere else in colour space (Green & Cheney in prep). 1 JND is a thing, 3 JNDs is not. A JND correlates to a certain amount of Euclidian Distance (ΔS) in colour space which depends on the location of colour space in which the JND is defined. The term JND should not be used unless it has been defined using behavioural experiments. Unless that’s the case ΔS is the correct term to use.
References:
Siddiqi, A., Cronin, T.W., Loew, E.R., Vorobyev, M. & Summers, K. 2004. Interspecific and intraspecific views of color signals in the strawberry poison frog Dendrobates pumilio. J. Exp. Biol. 207: 2471–85.
Vorobyev, M. & Osorio, D. 1998. Receptor noise as a determinant of colour thresholds. Proc. R. Soc. B Biol. Sci.265: 351–358.
Vorobyev, M, Brandt R., Peitsch D. Laughlin S. B, Menzel R. 2001. Colour thresholds and receptor noise: Behaviour and physiology compared. Vision Research. 41:639-653
